Algorithms for ensuring fault tolerance are key ingredients in many applications such as avionics, networking, transportation, and industrial plants. There is an increasing demand to integrate (formal) validation in the design process of these algorithms as they are often part of safety critical systems. When validation fails, the designer will benefit from tracking the sequence of events that led to an incorrect state to recover the error. To productively integrate formal verification in the design phase, tools should be able to return such error traces. Automating verification for fault tolerant algorithms turns out to be a daunting task as often they are parametric (i.e. they are designed to work with an arbitrary finite number of processes) so that checking that an algorithm satifies a certain property requires to prove it regardless of the number of processes.
In this paper, we propose the use of an infinite state model checker, called MCMT [1], for safety properties to assist in the design of this class of algorithms. MCMT is particularly suitable for this purpose because it is based on a declarative framework in which parametric algorithms can be naturally specified and uses the Satisfiability Modulo Theories (SMT) technology to automate their verification. SMT solvers have proved to be quite effective to tackle the verification of very large and complex systems. Roughly, the design phases consider the specification of the algorithm and of its safety property, the choice of the failure model in which the protocol should operate (e.g., crash-failure or send- omission), and finally the validation through the model checker. This schema can be nicely combined with a standard incremental and iterative approach to design. For example, the user can perform partial verifications during early development phases, change its failure model into a more realistic one, determine invariant properties of the system he is building, and so on, thereby getting various kinds of benefits from the automated support.
We applied the above methodology to formally check the agreement property of the reliable broadcast protocols of Chandra and Toueg [2]. The results of the model checker confirm those of the pen-and-paper proof in their published paper showing the practical viability of our technique.
In the next sections (Code section and Results section) there are respectively the files used with MCMT and some experimental statistics.
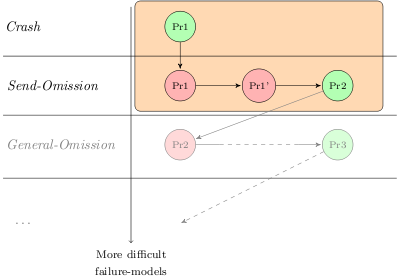
First of all, we have formalized the first protocol presented on [2] that works correctly with the Stopping-failure model. This protocol is represented in the figure by the green item in the Crash section labeled with Pr1, and is referenced in the next two sections as "1stprotocol, crash failures".
Following the iterative strategy used in [2], we have changed the failure-model of the environment - from the Stopping-failure model to the Send-Omission failure model - to show that the previous protocol is not safe in this new failure-model. This step is represented in the figure by the red item in the Send-Omission section labeled with Pr1, and is referenced in the next two sections as "1stprotocol, send-omission failures".
In order to overcome the failure of the previous protocol in this new failure-model, the authors of [2] initially propose the use of a negative acknowledgment (nack). Unfortunately this improvement is not sufficient to make the protocol safe. This step is represented in the figure by the red item in the Send-Omission section labeled with Pr1', and is referenced in the next two sections as "1stprotocol (edit), send-omission failures".
The authors of [2] propose another improvement for making the protocol safe w.r.t the Send-Omission failure-model.
With this new improvement, they show - no formal method is used, just informal reasoning (in natural language) on the algorithm behavior - that the protocol is safe.
In this case, however, MCMT reaches 50,000 nodes and then it stops the computation (this parameter is set by default). To work out this problem we searched seven invariants, that are:
- Exists only one coordinator in the system
- If c is coordinator, all other process with id < c have already been coordinator
- A coordinator can't have id[] greater than his identificator
- A process can't have id[] greater than coordinator's identificator
- In the first round a process can't have id[] equals to the coordinator's identificator
- A correct process can't receive any nack
- Coordinators are elected in order by identificator
This invariants are included as suggested invariants in all the formalizations further on discussed; MCMT will proove them to be real safe invariants before using them in the verification process. With this seven invariants MCMT is able to check the safety of the protocol. This step is represented in the figure by the green item in the Send-Omission section labeled with Pr2, and is referenced in the next two sections as "2nd protocol, no lemmas".
On [2], the authors use three lemmata to show some properties of the protocols. We have formalized and verified this three lemmata and then inserted them as system axioms in the files with the formalization. These three lemmata allow to save some resources during the verification processes, as showed in the experimental results table: the verification process with the three lemmata as system axioms generate 48 less nodes and makes 4,770 less calls to the SMT-solver (see "2nd protocol, with lemmas as system axioms" statistics)
The first lemma used in this experiments is little different from the lemma written on [2] (to write exactly the same lemma we needed an "hystorical variable", but this fact would complicate more the verification processes); our lemma is this:
let x be a process that received the estimate in round T-2 and a decide message in round T. Let y be the coordinator of the system and z another undecided correct process. When the system arrives in round T, z has the same estimate that y.
The set of configurations represented by the lemma 2.1 written on [2] is a proper subset of the set of configurations represented by our lemma.
The file (2nd protocol, with lemmas as system axioms) is a self-contained files without system axioms. In this files the three lemmata are written as multiple unsafe configurations.
| Protocol | High level language* | MCMT ready | ||||||
|---|---|---|---|---|---|---|---|---|
| *Follow this link to get the compiler for these files. | ||||||||
| 1st protocol, crash failures | [Download] | [Download] | ||||||
| 1st protocol, send-omission failures | [Download] | [Download] | ||||||
| 1st protocol (edit), send-omission failures | [Download] | [Download] | ||||||
| 2nd protocol, 1st lemma | [Download] | [Download] | ||||||
| 2nd protocol, 2nd lemma | [Download] | [Download] | ||||||
| 2nd protocol, 3rd lemma | [Download] | [Download] | ||||||
| 2nd protocol, no lemmas | [Download] | [Download] | ||||||
| 2nd protocol, with lemmas as system axioms | [Download] | [Download] | ||||||
| 2nd protocol, with lemmas as multiple unsafe configurations | [Download] | [Download] | ||||||
To get the compiler for the files written in the high level language follow this link.
The tool MCMT comes with a lot of options. The most important options for these experiments are those dealing with invariant generation. Athough the experiments reported in [1] have been obtained running the tool without specifying any option, in the following table we report all the experimental results obtained with MCMT and enabling different heuristics for invariant synthesis.
| Protocol | MCMT Result | INDEX vars | State vars | Transitions | Time (seconds)* | Max Depth | Nodes | Deleted nodes | SMT-solver calls | Invariants found | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| *Timings have been obtained on an Intel Core2 Duo @ 2.66 GHz with 2 Gb Sdram running Debian linux. MCMT (v. 1.0.1) has been executed without options. | |||||||||||
| 1st protocol, crash failures | SAFE | 4 | 8 | 13 | 1.18 | 13 | 113 | 21 | 2,792 | x | |
| 1st protocol, send-omission failures | UNSAFE | 5 | 9 | 16 | 17.66 | 12 | 464 | 26 | 19733 | x | |
| 1st protocol (edit), send-omission failures | UNSAFE | 6 | 11 | 22 | 1,624.24 | 34 | 9,679 | 770 | 1,338,058 | x | |
| 2nd protocol, 1st lemma | SAFE | 4 | 15 | 28 | 12.53 | 15 | 95 | 10 | 11,590 | 19 (+7) | |
| 2nd protocol, 2nd lemma | SAFE | 5 | 15 | 28 | 386.62 | 24 | 1,813 | 215 | 261,814 | 19 (+7) | |
| 2nd protocol, 3rd lemma | SAFE | 2 | 15 | 28 | 1.46 | 3 | 4 | 0 | 2,414 | 19 (+7) | |
| 2nd protocol, no lemmas | SAFE | 6 | 15 | 28 | 4,663.74 | 39 | 11,206 | 1,290 | 2,563,756 | 19 (+7) | |
| 2nd protocol, with lemmas as system axioms | SAFE | 6 | 15 | 28 | 4,719.51 | 39 | 11,158 | 1,290 | 2,558,986 | 19 (+7) | |
| 2nd protocol, with lemmas as multiple unsafe configurations | SAFE | 6 | 15 | 28 | 5,147.19 | 39 | 11,388 | 1,272 | 2,996,940 | 19 (+7) | |
| [1] | MCMT web page |
| [2] | T. D. Chandra and S. Toueg. Time and message efficient reliable broadcasts. In Proceedings of the 4th international workshop on Distributed algorithms, 289-303, 1991. |

